A polarização é uma das características básicas das antenas. Primeiro, precisamos entender a polarização de ondas planas. Em seguida, podemos discutir os principais tipos de polarização de antenas.
polarização linear
Vamos começar a entender a polarização de uma onda eletromagnética plana.
Uma onda eletromagnética (EM) plana possui diversas características. A primeira é que a energia se propaga em uma única direção (não há variação de campo em duas direções ortogonais). Em segundo lugar, o campo elétrico e o campo magnético são perpendiculares entre si e ortogonais entre si. Os campos elétrico e magnético são perpendiculares à direção de propagação da onda plana. Como exemplo, considere um campo elétrico de frequência única (campo E) dado pela equação (1). O campo eletromagnético se propaga na direção +z. O campo elétrico está direcionado na direção +x. O campo magnético está na direção +y.
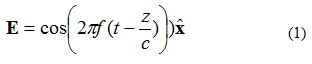
Na equação (1), observe a notação: . Este é um vetor unitário (um vetor de comprimento), que indica que o ponto do campo elétrico está na direção x. A onda plana é ilustrada na Figura 1.
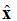
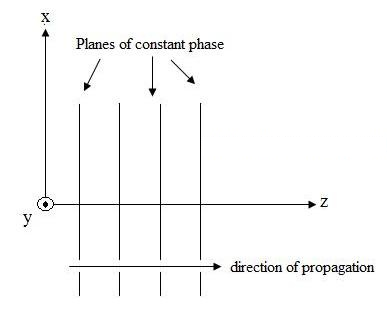
Figura 1. Representação gráfica do campo elétrico que se propaga na direção +z.
A polarização é o traço e a forma de propagação (contorno) de um campo elétrico. Como exemplo, considere a equação do campo elétrico de onda plana (1). Observaremos a posição onde o campo elétrico é (X,Y,Z) = (0,0,0) em função do tempo. A amplitude desse campo é mostrada na Figura 2, em vários instantes de tempo. O campo oscila na frequência "F".
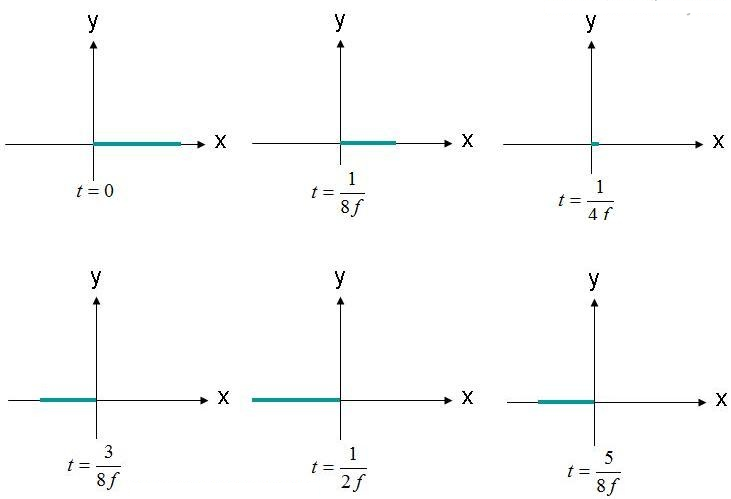
Figura 2. Observe o campo elétrico (X, Y, Z) = (0,0,0) em diferentes instantes de tempo.
O campo elétrico é observado na origem, oscilando em amplitude. O campo elétrico está sempre alinhado ao eixo x indicado. Como o campo elétrico se mantém ao longo de uma única linha, pode-se dizer que ele é linearmente polarizado. Além disso, se o eixo x for paralelo ao solo, esse campo também é descrito como horizontalmente polarizado. Se o campo estiver orientado ao longo do eixo y, a onda pode ser considerada verticalmente polarizada.
Ondas linearmente polarizadas não precisam estar direcionadas ao longo de um eixo horizontal ou vertical. Por exemplo, uma onda de campo elétrico com uma restrição ao longo de uma linha, como mostrado na Figura 3, também seria linearmente polarizada.
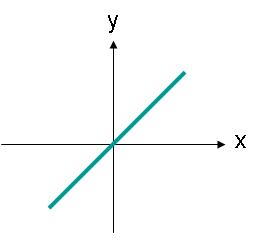
Imagem 3. A amplitude do campo elétrico de uma onda linearmente polarizada cuja trajetória forma um ângulo.
O campo elétrico na Figura 3 pode ser descrito pela equação (2). Agora, há uma componente x e uma componente y do campo elétrico. Ambas as componentes têm a mesma intensidade.
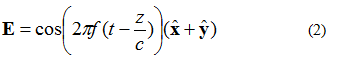
Um aspecto a observar na equação (2) é a componente xy e os campos eletrónicos na segunda fase. Isto significa que ambas as componentes têm a mesma amplitude em todos os momentos.
polarização circular
Agora suponha que o campo elétrico de uma onda plana seja dado pela equação (3):
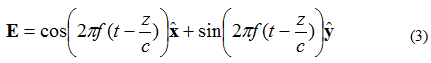
Neste caso, os elementos X e Y estão defasados em 90 graus. Se o campo for observado como (X, Y, Z) = (0,0,0) novamente como antes, a curva do campo elétrico em função do tempo aparecerá como mostrado abaixo na Figura 4.
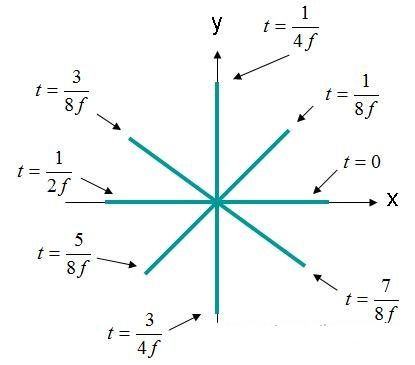
Figura 4. Intensidade do campo elétrico (X, Y, Z) = (0,0,0) domínio EQ. (3).
O campo elétrico na Figura 4 gira em um círculo. Esse tipo de campo é descrito como uma onda polarizada circularmente. Para que haja polarização circular, os seguintes critérios devem ser atendidos:
- Padrão para polarização circular
- O campo elétrico deve ter duas componentes ortogonais (perpendiculares).
- As componentes ortogonais do campo elétrico devem ter amplitudes iguais.
- Os componentes em quadratura devem estar defasados em 90 graus.
Ao percorrer a tela da Figura de Onda 4, diz-se que a rotação do campo é anti-horária e polarizada circularmente à direita (RHCP). Se o campo girar no sentido horário, ele terá polarização circular à esquerda (LHCP).
Polarização elíptica
Se o campo elétrico tiver duas componentes perpendiculares, defasadas em 90 graus, mas de mesma magnitude, o campo será elipticamente polarizado. Considerando o campo elétrico de uma onda plana que se propaga na direção +z, descrito pela Equação (4):
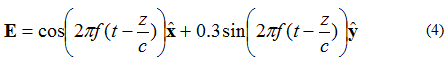
O lugar geométrico do ponto em que a extremidade do vetor do campo elétrico irá se concentrar é mostrado na Figura 5.
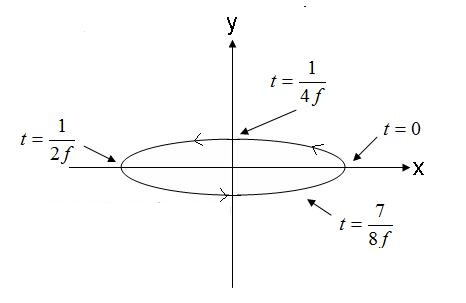
Figura 5. Campo elétrico da onda de polarização elíptica imediata. (4).
O campo na Figura 5, viajando no sentido anti-horário, seria elíptico dextrógiro se estivesse saindo da tela. Se o vetor do campo elétrico girar no sentido oposto, o campo será polarizado elipticamente levógiro.
Além disso, a polarização elíptica refere-se à sua excentricidade. A razão entre a excentricidade e a amplitude dos eixos maior e menor. Por exemplo, a excentricidade da onda, de acordo com a equação (4), é 1/0,3 = 3,33. Ondas polarizadas elipticamente são ainda descritas pela direção do eixo maior. A equação de onda (4) tem como eixo principal o eixo x. Observe que o eixo maior pode estar em qualquer ângulo do plano. O ângulo não precisa coincidir com os eixos X, Y ou Z. Finalmente, é importante notar que tanto a polarização circular quanto a linear são casos especiais de polarização elíptica. Uma onda polarizada elipticamente com excentricidade 1,0 é uma onda polarizada circularmente. Ondas polarizadas elipticamente com excentricidade infinita. Ondas polarizadas linearmente.
Polarização da antena
Agora que temos conhecimento dos campos eletromagnéticos de ondas planas polarizadas, a polarização de uma antena é definida de forma simples.
Polarização de antena: Uma avaliação do campo distante de uma antena, ou seja, a polarização do campo irradiado resultante. Portanto, as antenas são frequentemente classificadas como "polarizadas linearmente" ou "polarizadas circularmente à direita".
Este conceito simples é importante para comunicações por antena. Primeiro, uma antena polarizada horizontalmente não se comunicará com uma antena polarizada verticalmente. Devido ao teorema da reciprocidade, as antenas transmitem e recebem exatamente da mesma maneira. Portanto, antenas polarizadas verticalmente transmitem e recebem campos polarizados verticalmente. Logo, se você tentar transmitir um sinal de uma antena polarizada horizontalmente para uma antena polarizada verticalmente, não haverá recepção.
Em geral, para duas antenas linearmente polarizadas rotacionadas uma em relação à outra por um ângulo ( ), a perda de potência devido a essa incompatibilidade de polarização será descrita pelo fator de perda de polarização (PLF):
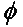
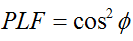
Portanto, se duas antenas tiverem a mesma polarização, o ângulo entre seus campos de elétrons radiantes será zero e não haverá perda de potência devido à incompatibilidade de polarização. Se uma antena for polarizada verticalmente e a outra horizontalmente, o ângulo será de 90 graus e nenhuma potência será transferida.
NOTA: Mover o telefone acima da cabeça em diferentes ângulos explica por que a recepção às vezes pode melhorar. As antenas de celulares geralmente são polarizadas linearmente, então girar o telefone pode muitas vezes igualar a polarização do aparelho, melhorando assim a recepção.
A polarização circular é uma característica desejável em muitas antenas. Ambas as antenas possuem polarização circular e não sofrem perda de sinal devido à incompatibilidade de polarização. As antenas utilizadas em sistemas GPS possuem polarização circular à direita.
Agora, suponha que uma antena linearmente polarizada receba ondas polarizadas circularmente. Equivalentemente, suponha que uma antena circularmente polarizada tente receber ondas linearmente polarizadas. Qual é o fator de perda de polarização resultante?
Lembre-se de que a polarização circular é, na verdade, composta por duas ondas linearmente polarizadas ortogonais, defasadas em 90 graus. Portanto, uma antena linearmente polarizada (LP) receberá apenas a componente de fase da onda circularmente polarizada (CP). Consequentemente, a antena LP terá uma perda por desajuste de polarização de 0,5 (-3 dB). Isso é válido independentemente do ângulo de rotação da antena LP.
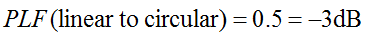
O fator de perda de polarização também é conhecido como eficiência de polarização, fator de desajuste de antena ou fator de recepção de antena. Todos esses nomes se referem ao mesmo conceito.
Data da publicação: 22 de dezembro de 2023







