Um refletor triédrico, também conhecido como refletor de canto ou refletor triangular, é um dispositivo passivo comumente usado em antenas e sistemas de radar. Consiste em três refletores planos que formam uma estrutura triangular fechada. Quando uma onda eletromagnética atinge um refletor triédrico, ela é refletida de volta na direção de incidência, formando uma onda refletida que tem a mesma direção, mas fase oposta à da onda incidente.
A seguir, apresentamos uma introdução detalhada aos refletores de canto triédricos:
Estrutura e princípio:
Um refletor de canto triédrico consiste em três refletores planos centrados em um ponto de interseção comum, formando um triângulo equilátero. Cada refletor plano é um espelho plano que pode refletir ondas incidentes de acordo com a lei da reflexão. Quando uma onda incidente atinge o refletor de canto triédrico, ela será refletida por cada um dos refletores planos, formando, eventualmente, uma onda refletida. Devido à geometria do refletor triédrico, a onda refletida é refletida na mesma direção, porém oposta à da onda incidente.
Funcionalidades e aplicações:
1. Características de reflexão: Os refletores de canto triédricos apresentam alta refletividade em determinada frequência. Eles refletem a onda incidente com alta refletividade, formando um sinal de reflexão nítido. Devido à simetria de sua estrutura, a direção da onda refletida pelo refletor triédrico é a mesma da onda incidente, porém em fase oposta.
2. Sinal refletido forte: Como a fase da onda refletida é oposta, quando o refletor triédrico está posicionado em direção oposta à da onda incidente, o sinal refletido será muito forte. Isso torna o refletor triédrico de canto uma aplicação importante em sistemas de radar para amplificar o sinal de eco do alvo.
3. Diretividade: As características de reflexão do refletor de canto triédrico são direcionais, ou seja, um sinal de reflexão forte será gerado apenas em um ângulo de incidência específico. Isso o torna muito útil em antenas direcionais e sistemas de radar para localização e medição da posição de alvos.
4. Simples e econômico: A estrutura do refletor de canto triédrico é relativamente simples e fácil de fabricar e instalar. Geralmente é feito de materiais metálicos, como alumínio ou cobre, o que reduz seu custo.
5. Áreas de aplicação: Os refletores de canto triédricos são amplamente utilizados em sistemas de radar, comunicações sem fio, navegação aérea, medição e posicionamento, entre outras áreas. Podem ser usados como antenas para identificação de alvos, telemetria, radiogoniometria e calibração, etc.
A seguir, apresentaremos este produto em detalhes:
Para aumentar a diretividade de uma antena, uma solução bastante intuitiva é usar um refletor. Por exemplo, se partirmos de uma antena de fio (digamos, uma antena dipolo de meia onda), podemos colocar uma folha condutora atrás dela para direcionar a radiação para a frente. Para aumentar ainda mais a diretividade, pode-se usar um refletor de canto, como mostrado na Figura 1. O ângulo entre as placas será de 90 graus.
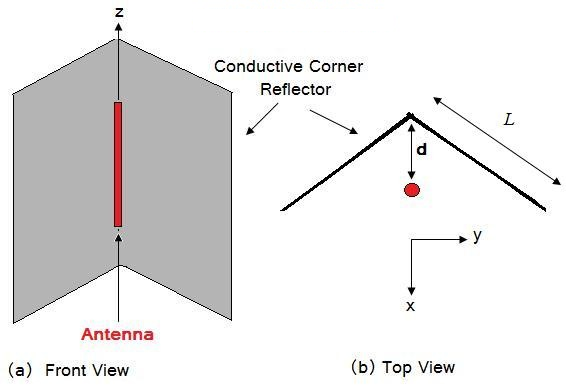
Figura 1. Geometria do refletor de canto.
O padrão de radiação desta antena pode ser compreendido utilizando a teoria de imagens e, em seguida, calculando o resultado através da teoria de arranjos. Para facilitar a análise, assumiremos que as placas refletoras têm extensão infinita. A Figura 2 abaixo mostra a distribuição de fonte equivalente, válida para a região em frente às placas.
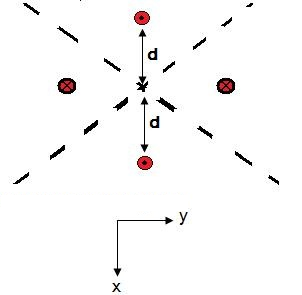
Figura 2. Fontes equivalentes no espaço livre.
Os círculos tracejados indicam antenas que estão em fase com a antena real; as antenas marcadas com um "x" estão 180 graus fora de fase com a antena real.
Suponha que a antena original tenha um padrão omnidirecional dado por ( ). Então o padrão de radiação (R) do "conjunto equivalente de radiadores" da Figura 2 pode ser escrito como:
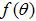
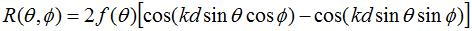
O exposto acima decorre diretamente da Figura 2 e da teoria de arranjos (k é o número de onda). O padrão resultante terá a mesma polarização da antena original polarizada verticalmente. A diretividade será aumentada em 9-12 dB. A equação acima fornece os campos irradiados na região em frente às placas. Como assumimos que as placas são infinitas, os campos atrás das placas são zero.
A diretividade será máxima quando d for meio comprimento de onda. Supondo que o elemento radiante da Figura 1 seja um dipolo curto com um padrão dado por ( ), os campos para este caso são mostrados na Figura 3.
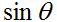
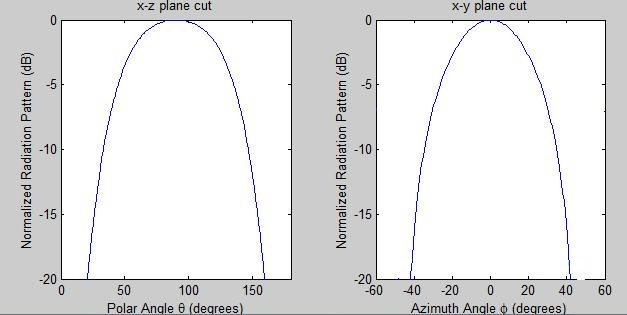
Figura 3. Padrões polares e azimutais do padrão de radiação normalizado.
O padrão de radiação, a impedância e o ganho da antena serão influenciados pela distância.dNa Figura 1, a impedância de entrada aumenta devido ao refletor quando o espaçamento é de meia onda; ela pode ser reduzida aproximando a antena do refletor. O comprimentoLOs refletores na Figura 1 são tipicamente 2*d. No entanto, se traçarmos um raio viajando ao longo do eixo y a partir da antena, este será refletido se o comprimento for pelo menos ( ). A altura das placas deve ser maior que o elemento radiante; contudo, como as antenas lineares não irradiam bem ao longo do eixo z, este parâmetro não é de importância crítica.
Refletor de canto triédricoApresentação da série de produtos:
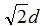
Data da publicação: 12 de janeiro de 2024













